കലനശാസ്ത്രത്തിന്റെ (calculus) ഘടകങ്ങൾ ഉൾപ്പെടെ, വളരെ പ്രാധാന്യമുള്ള പലഗണിതശാസ്ത്ര സമ്പ്രദായങ്ങളും 14–ഉം 16-ഉം നൂറ്റാണ്ടുകൾക്കിടയ്ക്ക് കേരളത്തിൽ രൂപപ്പെട്ടിരുന്നു. ഇക്കാലയളവിൽ കേരളം പുറംലോകവുമായി, കിഴക്ക് ചൈനയുമായും പടിഞ്ഞാറു അറേബ്യയുമായും നിരന്തര സമ്പർക്കം പുലർത്തിയിരുന്നു. ഒപ്പം 1499ലെ വാസ്കോ ഡ ഗാമയുടെ പുതിയ വഴിയൊരുക്കിയ ജലയാത്രയ്ക്ക് ശേഷം യൂറോപ്പുമായി നേരിട്ടൊരു മാർഗ്ഗവും സൃഷ്ടമായി. പഠനത്തിന്റെ ഇന്നത്തെ അറിവ് വെച്ച് ആശയവിനിമയത്തിന്റെ ഈ മാർഗ്ഗങ്ങൾ നിലനിന്നിരുന്നിട്ടും കേരളീയ കലനശാസ്ത്രം കേരളത്തിൽ മാത്രമായി ഒതുങ്ങി നിൽക്കുകയാണുണ്ടായത് എന്നാണു മനസ്സിലാക്കേണ്ടത്. കലനശാസ്ത്രത്തിന്റെ കേരളശാഖയുടെ വിജ്ഞാനസിദ്ധാന്തത്തെയും അത് യൂറോപ്പിലേക്ക് വ്യാപിച്ചതിനെപ്പറ്റിയുള്ള അനുമാനങ്ങളെയും കുറിച്ച് നിരീക്ഷിക്കുന്ന, നടന്നുകൊണ്ടിരിക്കുന്ന ഒരു ഗവേഷണത്തിന്റെ ഭാഗമായുള്ള കണ്ടെത്തലുകളെ അടിസ്ഥാനമാക്കിയുള്ളതാണു ഈ ലേഖനം.
1. ആമുഖം
പഠനമനുസരിച്ച് യൂറോപ്യൻ മാർഗ്ഗദർശികളായ ഫെർമാറ്റ്, റോബെർവാൽ, ടെയ്ലർ, ഗ്രിഗറി, പാസ്കൽ, ബെർണോളി എന്നിവരുടെ കണ്ടെത്തലുകളുടെ സഹായത്തോടെ പതിനേഴാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ ന്യൂട്ടന്റെയും ലയ്ബ്നിസിന്റെയും സ്വതന്ത്ര കണ്ടുപിടുത്തങ്ങളായാണു കലനശാസ്ത്രത്തിന്റെ പൊതുരീതികൾ ആവിഷ്കൃതമായത്. എന്നാൽ അധികം ആരും അറിയാത്ത കാര്യം pi എന്ന സംഖ്യയ്ക്കും sin x, cos x and tan-1 x എന്നീ ത്രികോണമിതി ഫലനങ്ങൾക്കും (ഗ്രിഗറി സീരീസ്) വേണ്ട അനന്തശ്രേണി അവകലനങ്ങൾ (infinite series derivations) സംഖ്യാസമാകലനസമ്പ്രദായങ്ങൾ (numerical integration methods) എന്നിവ പോലെയുള്ള കലനത്തിന്റെ അടിസ്ഥാനഘടകങ്ങൾ അതിനും 250നു മേലെ വർഷങ്ങൾക്കു മുൻപ് തന്നെ കേരളത്തിൽ കണ്ടുപിടിക്കപ്പെട്ടിരുന്നു എന്നുള്ളതാണു. ഈ വികാസങ്ങൾ ആദ്യം പ്രദർശിതമായത് കേരളഗണിതശാസ്ത്രജ്ഞനായിരുന്ന മാധവന്റെ കൃതികളിലായിരുന്നു. തുടർന്ന് 14-ഉം 16-ഉം നൂറ്റാണ്ടുകൾക്കിടയിൽ അദ്ദേഹത്തിന്റെ അനുയായികളായ നീലകണ്ഠ സോമയാജി, ജ്യേഷ്ഠദേവൻ, ശങ്കര വാര്യർ മുതലായവർ ആ ആശയങ്ങളെ കൂടുതൽ വിപുലവും വിസ്തൃതവുമാക്കുകയുമുണ്ടായി. ഇരുപതാം നൂറ്റാണ്ടിന്റെ രണ്ടാം പാദത്തിൽ ഇന്ത്യയ്ക്ക് പുറത്ത് ഈ യാഥാർത്ഥ്യം അല്പം അംഗീകൃതമായി. കേരള സ്കൂളിന്റെ ഈ പരിശ്രമങ്ങളെ അംഗീകരിക്കുന്ന അനേകം ആധുനിക യൂറോപ്യൻ ഗണിതശാസ്ത്രചരിത്രങ്ങൾ ഇന്ന് നിലവിലുണ്ട്. എങ്കിൽ തന്നെയും ഈ അംഗീകാരം സാർവത്രികമല്ല എന്നത് പ്രത്യേകം ശ്രദ്ധിക്കേണ്ടതാണു. ഉദാഹരണത്തിനു ഫീഗെൻബോമിന്റേതായി (Fiegenbaum) അടുത്തകാലത്ത് പ്രസിദ്ധീകരിച്ച കലനശാസ്ത്രത്തിന്റെ ചരിത്രം സംബന്ധിച്ച ഒരു പേപ്പറിൽ കേരളസ്കൂളിന്റെ സംഭാവനകളെക്കുറിച്ച് പരാമർശിക്കുന്നതേയില്ല. എന്നിരുന്നാലും ഫീഗെൻബോമിന്റെ പേപ്പർ പ്രസിദ്ധീകൃതമാകുന്നതിനു മുൻപ് തന്നെ കേരളീയ കലനശാസ്ത്രത്തിന്റെ ചരിത്രം വിശദമാക്കുന്ന കേൾവികേട്ട പല പ്രസിദ്ധീകരണങ്ങളും പടിഞ്ഞാറു ദൃശ്യമായിരുന്നു. കോളനിവൽക്കരണകാലത്ത് ചില യൂറോപ്യൻ രാജ്യങ്ങൾ രൂപപ്പെടുത്തിയ യൂറോപ് കേന്ദ്രീകൃത വീക്ഷണകോണുകളുടെ ഫലമാവാം ഈ നിരാസം എന്നാണു ഊഹിക്കേണ്ടത്.
2. ഇന്ത്യൻ – കേരളീയ ഗണിതത്തെക്കുറിച്ചുള്ള യൂറോപ്യൻ വീക്ഷണങ്ങൾ
രണ്ടാം സഹസ്രാബ്ദത്തിന്റെ ആദ്യഘട്ടങ്ങളിൽ ഇന്ത്യൻ ഗണിതത്തിന്റെ, കൃത്യമായി പറഞ്ഞാൽ ജ്യോതിശാസ്ത്രത്തിന്റെ, വിലയിരുത്തലുകൾ മിക്കവാറും തന്നെ നടത്തിയിരുന്നത് അറബ് വ്യാഖ്യാതാക്കളാണു. ഇന്ത്യൻ ഗണിതവും ശാസ്ത്രവും സ്വതന്ത്രശാഖകളായാണു ഉത്ഭവിച്ചത് എന്ന് അവർ സൂചിപ്പിച്ചു. സെയ്ദ് അൽ –ആൻഡലുസിയെപ്പോലുള്ള ചിലർ അവ ഉയർന്ന നിലവാരത്തിലുള്ളവയാണെന്ന് അഭിപ്രായപ്പെട്ടു:
“[ഭാരതീയർ] നക്ഷത്രചലനങ്ങളെക്കുറിച്ചും (ജ്യോതിശാസ്ത്രം) ആകാശങ്ങളുടെ രഹസ്യത്തിന്മേലും (ജ്യോതിഷം) മറ്റു ഗണിതശാസ്ത്രസംബന്ധിയായ വിഷയങ്ങളിലും അപാരമായ പാണ്ടിത്യം നേടുക വഴി അറിവിന്റെ മേഖലയിൽ അത്യുന്നതിയിലെത്തിയിട്ടുണ്ട്. ഒപ്പം തന്നെ വൈദ്യശാസ്ത്രരംഗത്തും പലവിധ ഔഷധങ്ങളുടെ വീര്യം സംബന്ധിച്ചും, സംയുക്തങ്ങളുടെ സ്വഭാവവിശേഷങ്ങളെക്കുറിച്ചും വസ്തുക്കളുടെ വൈചിത്ര്യങ്ങളെക്കുറിച്ചുമുള്ള അറിവിൽ മറ്റെല്ലാവരെയും പിന്നിലാക്കുകയും ചെയ്തിരിക്കുന്നു.”
അല്പം കൂടി വിമർശനാത്മകമായിരുന്നു ആൽബറൂണിയെപ്പോലെയുള്ളവരുടെ നിരീക്ഷണം. ഇരുപത്തൊന്നാം നൂറ്റാണ്ടിലെ വിശാലമായ ഗണിതശാസ്ത്രസാഹിത്യം പോലെ, അല്പം മാത്രം മികച്ചവയും മിക്കവാറും തന്നെ പിശകുകളും നിറഞ്ഞ ഗവേഷണപ്രബന്ധങ്ങളാൽ നിറഞ്ഞ്നിമ്നോന്നതമായിരുന്നു ഇന്ത്യൻ ഗണിതത്തിന്റെയും ജ്യോതിശാസ്ത്രത്തിന്റെയും ഭൂമിക എന്നദ്ദേഹം സമർത്ഥിച്ചു: “ഞാൻഅറിഞ്ഞിടത്തോളം പിയർ പഴങ്ങളും കയ്ക്കുന്ന ഈന്തപ്പഴങ്ങളും, അല്ലെങ്കിൽ മുത്തുകളും ചാണകവും പോലെ, അതുമല്ലെങ്കിൽ വിലപിടിപ്പുള്ള പരലുകളും സാദാ വെള്ളാരംകല്ലുകളും പോലെ ഒരു മിശൃതമാണു ഇന്ത്യൻ ഗണിത, ജ്യോതിശാസ്ത്രസാഹിത്യം.
എന്തു തന്നെയായാലും ഈ ആദ്യകാല വിലയിരുത്തലുകളുടെയെല്ലാം പൊതുസ്വഭാവം ഇന്ത്യൻ ഗണിതത്തിന്റെ വികാസത്തെ അവ ചൂണ്ടിക്കാട്ടിയിരുന്നു എന്നതാണു. എന്നാൽ പത്തൊൻപതാം നൂറ്റാണ്ടോടെ, കിഴക്ക് യൂറോപ്യൻ കോളണികൾ സ്ഥാപിതമാകുന്നതിനു സമകാലീനമായി, യൂറോപ്യൻ വിജ്ഞാനത്തിനു അവർ തന്നെ കല്പിച്ചിരുന്ന അധീശത്വത്തെ സംബന്ധിച്ചുള്ള യൂറോപ്യൻ പണ്ഡിതലോകത്തിന്റെ ധാരണകൾക്ക് വംശീയമായ ഒരു മാനം കൈവരാൻ ആരംഭിച്ചു. ഇന്ത്യൻ ശാസ്ത്രം മാത്രമല്ല യൂറോപ്പിനോട് കടപ്പെട്ടിരിക്കുന്നതെന്നും ഇന്ത്യൻ സംഖ്യകൾ റോമൻ സംഖ്യകളുടെ ചുരുക്കി എഴുതിയ രൂപങ്ങളാണെന്നും സംസ്കൃതം കലങ്ങിമറിഞ്ഞ ഗ്രീക്കാണെന്നും ഇന്ത്യയ്ക്ക് കാലഗണനം അന്യമായിരുന്നുവെന്നും സെഡില്ലൊട്ട് (Sedillot) സമർത്ഥിച്ചു. അദ്ദേഹത്തിന്റെ വിവരണങ്ങൾ ഇന്ത്യൻഗണിതത്തിന്റെ വ്യാപ്തിയേയും വിശേഷഗുണങ്ങളെക്കുറിച്ചുമുള്ള വികലവും അപൂർണ്ണവുമായ അറിവുകളുടെ അടിസ്ഥാനത്തിലായിരുന്നു എന്നുള്ളതൊന്നും “ഒരുവശത്ത് സമ്പൂർണ്ണമായ ഒരു ഭാഷയുണ്ട്, അനേകം നൂറ്റാണ്ടുകളായി മനുഷ്യന്റെ എല്ലാ സാംസ്കാരിക അറിവുകളാലും അംഗീകരിക്കപ്പെട്ട, കലകളിലൂടെ പൂർണ്ണതയുടെ ഔന്നത്യങ്ങളിലേക്ക് എത്തപ്പെട്ട, ഹോമറുടെ ഭാഷ. മറുവശത്ത് (ഇന്ത്യയിൽ)അനേകം ഭാഷാഭേദങ്ങളുള്ള തമിഴും ഇക്കാലം വരെ നിലനിന്ന, ഏറ്റവും അപരിഷ്കൃതങ്ങളായ അന്ധവിശ്വാസങ്ങളുടെ പരിതസ്ഥിതിയിൽ നില നിന്ന ആ ബ്രാഹ്മണിക അശ്ലീലതകളും.” എന്ന് പ്രസ്താവിക്കുന്നതിൽ നിന്ന് അദ്ദേഹത്തെ തടസപ്പെടുത്തിയില്ല.
സമാനമായി ബെന്റ്ലിയും (Bentley) ആര്യഭടനെയും മറ്റ് ഇന്ത്യൻ ഗണിതശാസ്ത്രകാരന്മാരെയും യഥാർത്ഥത്തിൽ അവർ ജീവിച്ചിരുന്നതിൽ നിന്ന് പല നൂറ്റാണ്ടുകൾ മാറ്റി ചിത്രീകരിച്ചുകൊണ്ട് ഇന്ത്യൻ കാലഗണനയിൽ സംശയങ്ങളുടെ നിഴൽ വീഴ്ത്തി. ഇന്ത്യൻഗണിതകാരന്മാർ അവരുടെ യഥാർത്ഥ കാലഘട്ടങ്ങളെക്കാൾ വളരെ മുൻപെ തന്നെ ജീവിച്ചിരുന്നു എന്നു കാണിക്കുന്നതിനു ബ്രാഹ്മണർ കൃത്രിമമായി തെളിവുകൾ സൃഷ്ടിച്ചിരുന്നു എന്നായിരുന്നു അദ്ദേഹത്തിന്റെ അഭിപ്രായം. “മറ്റൊരു കൃത്രിമത്വം കൂടി നമ്മുടെ ശ്രദ്ധയിൽ പെടുന്നു: ബ്രഹ്മസിദ്ധാന്ത സ്ഫുടം. അതെഴുതിയതാരാണെന്ന് എനിക്കറിയാം. വാസ്തവത്തിൽ അക്ബറിന്റെ കാലത്ത്ജീവിച്ചിരുന്ന വരാഹമിഹിരനെ പൗരാണികതയിലേക്ക് മാറ്റി പ്രതിഷ്ഠിക്കാനാണു ഈ കൃത്രിമനിർമ്മാണം…തത്ഫലമായി ആര്യഭടനെക്കാളും വരാഹമിഹിരനെക്കാളും വളരെക്കാലം മുൻപ് ജീവിച്ചിരുന്ന ബ്രഹ്മഗുപ്തൻ, അവരെ രണ്ടു പേരേയും പൗരാണികതയിലേക്ക് പ്രതിഷ്ഠിക്കുന്നതിനുള്ള ലക്ഷ്യത്തിന്റെ ഫലമായി, രണ്ട് പേരെയും ഉദ്ധരിക്കുന്നത് എങ്ങനെ എന്ന് കാണാൻ കഴിയുന്നു…ബ്രഹ്മസിദ്ധാന്തവും, അല്ലെങ്കിൽ അതിന്റെ ഒരു ഭാഗമെങ്കിലും, മറ്റു പലേ പുസ്തകങ്ങളെയും പോലെ കഴിഞ്ഞ നൂറ്റാണ്ടിലെ ഒരു ഗൂഢസംഘം ബ്രാഹ്മണരാൽ ക്രമത്തിലും ഉള്ളടക്കത്തിലും വ്യവസ്ഥാനുസൃതവുമായ ഒരു കപടനിർമ്മിതിയുടെ ഭാഗമായി സൃഷ്ടമായവയാണു.”
വാസ്തവത്തിൽമേൽ പ്രസ്താവിച്ചവരുടെ യഥാർത്ഥ ജീവിതകാലഘട്ടം ആര്യഭടൻ b 476 AD, വരാഹമിഹിരൻ c 505, ബ്രഹ്മഗുപ്തൻ c 598, അക്ബർ c 1550 എന്നിങ്ങനെയായിരുന്നു എന്നത് ഓർക്കേണ്ടതുണ്ട്. അതിനാൽ തന്നെ ബെന്റ്ലിയുടെ അനുമാനം അജ്ഞതയിൽ അടിസ്ഥാനപ്പെടുത്തിയുള്ളതോ യൂറോകേന്ദ്രീകൃത ശാസ്ത്രചരിത്രത്തിന്റെ കൃത്രിമനിർമിതികളിൽ ഒന്നോ ആണെന്ന് ആരോപിക്കുന്നതിനു ന്യായങ്ങളുണ്ട്. എന്തുതന്നെയായാലും ബെന്റ്ലി തിരുത്തിച്ചേർത്ത കാലനിർണ്ണയം ഇന്ത്യൻ ഗണിതത്തിന്റെ നേട്ടങ്ങൾ കുറയ്ക്കുന്നതിലും യൂറോപ്പിലേക്കുള്ള അതിന്റെ സംപ്രക്ഷണം വലിയ രീതിയിൽ അവ്യക്തമാക്കുന്നതിനും കാരണമായി.
ഇന്ത്യൻ ഗണിതത്തെപ്പറ്റിയുള്ള അപര്യാപ്തമായ അറിവ് മിൽ പണ്ഡിതരിൽ മാത്രം ഒതുങ്ങിനിന്നിരുന്നില്ല. അത്ര അകലെയല്ലാത്ത ഒരു കാലത്താണു വിഖ്യാത ഗണിതശാസ്ത്രചരിത്രകാരനായിരുന്ന സ്മിത്ത് 18, 19 നൂറ്റാണ്ടുകളിൽ രൂപപ്പെട്ട പടിഞ്ഞാറൻ സംസ്കാരമില്ലായിരുന്നുവെങ്കിൽ ഇന്ത്യ ഗണിതത്തിന്റെ ലോകത്ത് നിഷ്ക്രിയമായിപ്പോയേനെ എന്ന് അഭിപ്രായപ്പെട്ടത്. “ഭാസ്കരനു ശേഷം ( ഭാസ്കരൻ II, b. 1114) ഇന്ത്യ തദ്ദേശീയരായ പ്രതിഭാശാലികളെയൊന്നും തന്നെ ഈ രംഗത്തിനു സംഭാവന ചെയ്തില്ല” എന്നു പോലും അദ്ദേഹം പ്രസ്താവിക്കുകയുണ്ടായി.
യൂറോപ്പിതരലോകത്തെ ഗണിതശാസ്ത്രജ്ഞന്മാരുടെ കണ്ടെത്തലുകളും ആ ഗണിതശാസ്ത്രലോകങ്ങളിലുണ്ടായ പുരോഗതിയും അവഗണിക്കുന്ന രീതിയാണു ഈയടുത്ത കാലംവരെ നിലവിലിരുന്നത്. ഉദാഹരണത്തിനു എഡ്വാർഡിന്റെ കലനശാസ്ത്രചരിത്രത്തിലോ ഗണിതശാസ്ത്രചരിത്രകാരന്മാരായ അബെലെസിന്റെയും ഫീഗെൻബോമിന്റെയും അനന്യശ്രേണിയുടെ ചരിത്രത്തെപ്പറ്റിയുള്ള ലേഖനങ്ങളിലോ കേരളീയ സ്കൂളിന്റെ സംഭാവനയെപ്പറ്റി ഒന്നും തന്നെ പറയുന്നില്ല. യൂറോപ്യൻ കോളനിവൽക്കരണത്തിനു സമാന്തരമായി സൃഷ്ടമായ യൂറോകേന്ദ്രീകൃത കാഴ്ചപാടുകളാകാം അമ്പരപ്പിക്കുന്നവിധമുള്ള ഈ പക്ഷപാതത്തിന്റെ കാതൽ. അതിന്റെ ഫലമായി മറ്റ് പലകാര്യങ്ങളിലും എന്ന പോലെ ഗണിതശാസ്ത്രത്തിന്റെ ചരിത്രരചനയിലും വെള്ളക്കാരന്റെ അധീശത്വം എന്ന ആശയം പ്രകടമായി തീർന്നു. പത്തൊൻപതാം നൂറ്റാണ്ടിലെ യൂറോപ്പിൽ രൂപപ്പെട്ട ദേശീയതയുടെ ഉദയവും തൽഫലമായി യൂറോപ്യൻസംസ്കാരത്തിന്റെ വേരുകളെക്കുറിച്ചു നടന്ന അന്വേഷണങ്ങളുടെയും ഫലമായി ഒരു ഗ്രീക്ക് ബാധ നിലവിൽ വരികയും സകല വിജ്ഞാനത്തിന്റെയും മൂല്യങ്ങളുടെയും കളിത്തൊട്ടിലും ഗ്രീസാണെന്ന ധാരണ ശക്തമാകുകയും ചെയ്തു. യൂറോപ്പ് അതിനെ ഗ്രീക്ക് വിജ്ഞാനത്തിന്റെയും മൂല്യങ്ങളുടെയും പിന്തുടർച്ചാവകാശിയായി സ്വയം കണക്കാക്കാനും ആരംഭിച്ചു. ചരിത്രത്തിന്റെ വക്രീകൃതമായ ഇത്തരംവ് യാഖ്യാനങ്ങൾക്ക് അപൂർവ്വങ്ങളായി മാത്രമുണ്ടായ അപവാദം എബെനെസെർബർഗെസ്സിന്റെയും ജോർജ് പീക്കോക്കിന്റെയും വകയായിരുന്നു. അവർ യഥാക്രമം എഴുതി:
“പ്രഫസർ വൈറ്റ്നിയുടെ അഭിപ്രായം കണ്ടാൽ ഹിന്ദുക്കൾ അവരുടെ ജ്യോതിഷവും ജ്യോതിശാസ്ത്രവും ഗ്രീക്കുകാരിൽ നിന്ന് നേരിട്ട് കൈക്കലാക്കുകയായിരുന്നു എന്ന് തോന്നും… ഞാൻ കരുതുന്നത് അദ്ദേഹം ഹിന്ദുക്കൾക്ക് ആവശ്യത്തിനു മതിപ്പ് കൊടുക്കുന്നില്ല എന്നാണു. ഗ്രീക്കുകാർക്ക് അവരർഹിക്കുന്നതിൽ കൂടുതൽ അംഗീകാരം കൊടുക്കുകയും ചെയ്യുന്നു”
“വസ്തുതകളുടെ പിന്തുണ അല്പം പോലുമില്ലാത്ത [സംഖ്യകളുടെ ഗ്രീക്ക് ഉത്ഭവത്തെയും അവയുടെ ഇന്ത്യയിലേക്കുള്ള സംപ്രക്ഷണത്തെയും കുറിച്ചുള്ള] അനുമാനങ്ങൾക്ക് അനുകൂലമായി എഴുതിയിരിക്കുന്ന സമുന്നതരായ ആളുകൾ കൂടുതൽ ഉദാഹരണങ്ങൾ അതേപ്പറ്റി നിരത്തുന്നത് അനാവശ്യമാണെന്നു കരുതിയിരിക്കുകയാണെന്ന് തോന്നുന്നു”
എന്നിരുന്നാലും ഇരുപതാം നൂറ്റാണ്ടിന്റെ രണ്ടാം പാദത്തോടെ കോളനിവൽക്കരണത്തിന്റെ ശക്തമായ പ്രഭാവങ്ങളിൽ നിന്ന് മോചിതമായ യൂറോപ്യൻ പണ്ഡിതലോകം കേരളീയ സ്കൂളിന്റെ ഗണിതം രാജഗോപാലും പങ്കാളികളും പോലെയുള്ള ദ്വിതീയ ഉറവിടങ്ങൾ ഉപയോഗിച്ച്പരിശോധിക്കുവാൻ ആരംഭിച്ചു. കേരളസ്കൂളിന്റെ നേട്ടങ്ങളും യൂറോപ്പിലെ സമാനമായ വികാസങ്ങൾക്കുമേൽ അതിനു അവകാശപ്പെടാൻ കഴിയുന്ന പഴമയും അപ്പോഴേക്കും നിരവധി പടിഞ്ഞാറൻ പ്രസിദ്ധീകരണങ്ങളിൽ വന്നു തുടങ്ങിയിരുന്നു. എന്നാൽ ഈ വിലയിരുത്തലുകൾക്കൊപ്പം തന്നെ പൊതുകലനത്തിന്റെ കണ്ടുപിടിത്തം നടന്നത് യൂറോപ്പിലാണു എന്ന വാദവും ശക്തമായി ഉന്നയിക്കപ്പെട്ടു.
ഉദാഹരണത്തിനു ബാരൺ (Baron) പറയുന്നു:“ചില തരം അനന്യശ്രേണികളുടെയും കലനത്തിന്റെയും അവകലനത്തിന്റെയും ക്രിയാപദ്ധതികളിൽ ചില സാമാന്യവൽക്കരണവും ഒരുപ്രത്യേകരീതിയിൽ അവയെ ചിഹ്നവൽക്കരിക്കുകയും ചെയ്തു എന്നകേരളീയഗണിതത്തിന്റെയും സംഖ്യാകലനത്തിന്റെയും വികാസപരിണാമങ്ങളെയും അവയുടെപ്രയോഗവും സംബന്ധിച്ചുള്ള വിശ്വാസങ്ങളുമായി ബന്ധപ്പെട്ടാണു ലയ്ബ്നിസ്–ന്യൂട്ടൺ വിവാദം എങ്കിലും അവ മാത്രം മുൻനിർത്തി കലനശാസ്ത്രത്തിന്റെകണ്ടുപിടുത്തം അവർക്ക് അവകാശപ്പെട്ടതാണെന്ന് പറയുവാൻ കഴിയുന്നതല്ല” കാലിംഗർ (Calinger) എഴുതുന്നു:“ത്രികോണമിതിയിലെഫലനം എന്ന സങ്കല്പം പോലെ വളരെ നിസാരമായ ചിഹ്നസമ്പ്രദായം പോലുംകേരളഗണിതകാരന്മാർക്ക് അന്യമായിരുന്നു. എന്തുതന്നെയായാലുംജ്യോതിശാസ്ത്രപട്ടികകൾ തയ്യാറാക്കുന്നതിനപ്പുറം അവർ വിപരീതത്രികോണമിതിയിലെപാതി ചാണുകളുടെ പ്രാധാന്യമോ കലനത്തിന്റെ ആദ്യ രണ്ട് പതിപ്പുകൾ തയ്യാറാക്കവെന്യൂട്ടണും ലയ്ബ്നിസും അവ തമ്മിൽ കണ്ടെത്തിയ ബന്ധങ്ങളും അവർതിരിച്ചറിഞ്ഞിരുന്നോ? സ്പഷ്ടമായും ഇല്ല എന്നാണുത്തരം.
ഈതാരതമ്യങ്ങൾ പൊതു അനന്താംശ കലനത്തിന്റെ (generalised infinitesimal calculus) ഉപജ്ഞാതാക്കൾ എന്ന സ്ഥാനത്ത് ന്യൂട്ടണെയും ലയ്ബ്നിസിനെയുംസംരക്ഷിക്കുക എന്ന ഉദ്ദേശത്തോടെയുള്ളവയാണു. ശാസ്ത്രകാരന്മാരുടെനേട്ടങ്ങളുടെ പരിശോധനകളിൽ കാണാവുന്ന ശക്തമായ ദേശീയതാബോധത്തെക്കുറിച്ച് നമുക്കറിയാമെങ്കിലുംരണ്ട് വ്യത്യസ്ത വിജ്ഞാനസിദ്ധാന്തങ്ങളിലായി രൂപം കൊണ്ട രണ്ട്വികാസപരിണാമങ്ങളെ ഗുണാത്മകമായി താരതമ്യപ്പെടുത്താൻ നമുക്ക്ബുദ്ധിമുട്ടുകളുണ്ട്. സാമാന്യവൽക്കരണം പ്രധാനവും അനന്തം എന്നത് പ്രയാസകരമായഒരു വിഷയവുമായിരുന്ന യൂക്ലിഡിയൻ ജ്യാമിതിയുടെ മാതൃകകളിലാണു പതിനേഴാംനൂറ്റാണ്ടിലെ യൂറോപ്യൻ കലനത്തിന്റെ ആദ്യകാല പരിണാമങ്ങൾ സംഭവ്യമായതെന്നത്ഇവിടെ ഓർപ്പിക്കുന്നത് ഉചിതമായിരിക്കും. മറുഭാഗത്ത് 15ആം നൂറ്റാണ്ടുമുതൽക്ക് തന്നെ കേരളീയ ഗണിതകാരന്മാർ അഭികലനഗണിതത്തിൽ അനന്താംശം (infinitesimal) എന്ന ആശയം മനസ്സിലാക്കുന്നതിനും ചില പ്രത്യേകഫലനങ്ങൾക്കായുള്ള (functions) അനന്തശ്രേണി (infinite series) അവകലനങ്ങൾക്കും (derive) പ്ലവബിന്ദു സംഖ്യകൾ (floating point numbers)ഉപയോഗിച്ചുവന്നിരുന്നു (Whish, 1835). ഒരേതരം കാര്യങ്ങൾഅന്വേഷിക്കുന്നതിനു രണ്ട് കാലഘട്ടങ്ങളിലായുള്ള, ഗുണപരമായിവ്യത്യാസപ്പെട്ടിരിക്കുന്ന രണ്ട് തരം ബൗദ്ധികയുക്തികളെ ആശ്രയിക്കുക എന്നത്ഗുണപരമായി തന്നെ വ്യത്യസ്തമായ ഫലങ്ങളാകും തരിക എന്നാണു ഞങ്ങൾ സ്പഷ്ടമായുംകരുതുന്നത്. അതിനാൽ കേരളീയ ഗണിതത്തിനെ മനസ്സിലാക്കേണ്ടത് അത് വികസിച്ചഅതിന്റെ സ്വന്തം വിജ്ഞാനപദ്ധതികളുടെ പാതകളിലാണു. അല്ലാത്ത പക്ഷം ഷേക്സ്പിയർകൃതികളുടെ ഒരു സമ്പൂർണ്ണആസ്വാദനത്തിനായി ആ കൃതികളെ ഉർദുവിലേക്ക് വിവർത്തനംചെയ്യുന്നതുപോലെയായിരിക്കും അത്. വാഗാർത്ഥങ്ങളും (അർത്ഥവിജ്ഞാനീയം- semantic) സാംസ്കാരികവ്യജ്ഞനങ്ങളും നിശ്ചയമായും അതിൽ നഷ്ടമാകും.
3. സംപ്രക്ഷണത്തിനു മേൽ ഒരു ചർച്ച:
ശാസ്ത്രത്തിന്റെസംപ്രക്ഷണം എന്ന വസ്തുത ഉറപ്പിക്കുന്നതിനു ബന്ധപ്പെട്ടകയ്യെഴുത്തുപ്രതികളുടെ വിവർത്തനങ്ങൾ എന്ന പ്രത്യക്ഷവും നേരെയുള്ളതുമായതെളിവുകളെ ആശ്രയിക്കാവുന്നതാണു. ക്രിസ്തുവിനു ശേഷമുള്ള ആദ്യ നൂറ്റാണ്ടുകളിൽഅറബ് പണ്ഡിതർ വഴി നടന്ന ഇന്ത്യൻ ഗണിതശാസ്ത്രത്തിന്റെയുംജ്യോതിശാസ്ത്രത്തിന്റെയും യൂറോപ്പിലേക്കുള്ള സംപ്രക്ഷണം നേരിട്ടുള്ളതെളിവുകൾ കൊണ്ട് വസ്തുതാപരമെന്ന് സ്ഥാപിതമായ കാര്യമാണു. 662 എ ഡിയിൽയൂഫ്രട്ടീസ് മേഖലയിലെത്തിയിരുന്നു എന്നതിനാൽ 7-ആം നൂറ്റാണ്ടിന്റെആദ്യകാലങ്ങളിലെങ്കിലും ഇന്ത്യൻ സംഗണനസമ്പ്രദായങ്ങൾ (computational techniques) അതിന്റെ സംപ്രക്ഷണം ആരംഭിച്ചിരിക്കണം. ഇന്ത്യൻസംഗണനസമ്പ്രദായങ്ങളുടെ യൂറോപ്പിലേക്കുള്ള സഞ്ചാരത്തെക്കുറിച്ച്ബെനെഡിക്റ്റിന്റെ വകയായി ഒരു പ്രബന്ധമുണ്ട്. 760 എ ഡി യിൽ അറബിയിലേക്ക്സിദ്ധാന്തങ്ങളുടെ ഒരു പകർപ്പ് വിവർത്തനം ചെയ്യപ്പെടുക വഴി ഇന്ത്യൻ ജ്യോതിശാസ്ത്രം പടിഞ്ഞാറു ഇറാക്കിലേക്കും തുടർന്ന്സ്പെയിനിലേക്കും പടർന്നു. ഇന്ത്യൻ ഗണിതശാസ്ത്ര രചനകളുടെകയ്യെഴുത്തുപ്രതികളെക്കുറിച്ചുള്ള ആധികാരികരേഖകൾ ചൈനയിൽ നിന്നും തായ്ലൻഡിൽനിന്നും മറ്റ് തെക്കുകിഴക്കനേഷ്യൻ മേഖലകളിൽ നിന്നും 7 ആം നൂറ്റാണ്ടുമുതൽക്കു തന്നെ ലഭ്യമായിട്ടുണ്ട് എന്നതിനാൽ ഈ പടർച്ച പടിഞ്ഞാറേയ്ക്ക് മാത്രമായിരുന്നില്ല എന്നതും മനസ്സിലാക്കേണ്ടതുണ്ട്.
പൊതുവിലുള്ള രീതിയനുസരിച്ച് അത്തരംനേരിട്ടുള്ള തെളിവുകളുടെ അഭാവങ്ങളുള്ളപ്പോൾ സംപ്രക്ഷണംശരിയെന്ന് സ്ഥാപിക്കുവാൻ താഴെക്കൊടുത്തിട്ടുള്ളവ മതിയാകും.
i) പദ്ധതികളിലെ സമാനതകൾ കണ്ടെത്തൽ
ii)ആശയവിനിമത്തിന്റെ യാത്രാമാർഗ്ഗങ്ങൾ ഉണ്ടായിരിക്കുക
iii)സം പ്രക്ഷണത്തിനു യോജിച്ച ഒരു കാലനിർണ്ണയം.
അതുകൂടാതെ വിജ്ഞാനത്തിന്റെ ( പ്രധാനമായും ഗ്രീക്കിന്റെ)സം പ്രക്ഷണം സാധൂകരിക്കുന്നതിനായി വാൻ ഡെർ വേർഡെന്റെ ‘പൊതു ഉത്പത്തി സംബന്ധിച്ച അനുമാനം’ (‘hypothesis of a common origin’) എന്ന അനുമാനവുമുണ്ട്.സിദ്ധാന്തങ്ങളിൽപറഞ്ഞിരിക്കുന്ന ജ്യോതിശാസ്ത്രത്തിന്റെ ഗ്രീക്ക്ശ്രോതസ്സുകളെക്കുറിച്ചുള്ള തന്റെ ഊഹങ്ങൾ സ്ഥാപിക്കുന്നതിനു നോഗെബൗർ (Neugebauer) സ്വന്തം മാതൃകകളെയാണു ആശ്രയിക്കുന്നത്. അതേ പോലെ തന്നെആര്യഭടന്റെ ത്രികോണമിതി ഗ്രീസിൽ നിന്നും കടം കൊണ്ടതാണെന്ന്വാദിക്കുന്നതിനായി വാൻ ഡെർ വേർഡൻ ആശ്രയിക്കുന്നത്‘പൊതു ഉത്പത്തി സംബന്ധിച്ച അനുമാന’ത്തെയാണു . Diophantine സമവാക്യങ്ങളിന്മേലുള്ള ഭാസ്കരന്റെ പഠനങ്ങളെക്കുറിച്ചും വാൻഡെ വേർഡെൻ സമാനമായ വാദങ്ങൾ ഉന്നയിക്കുന്നുണ്ട്. അവ തമ്മിൽപദ്ധതിശാസ്ത്രപരമായ സമാനതകളുണ്ടെന്ന് ഉന്നയിക്കുമ്പോഴും അതിനുമപ്പുറംഭാസ്കരനും ശിഷ്യർക്കും ലഭ്യമായിരുന്ന, നമുക്കിതുവരെയും അജ്ഞാതമായ ഒരു ഗ്രീക്ക് ഗ്രന്ഥത്തിന്റെ അസ്തിത്വത്തിൽഅദ്ദേഹത്തിന്റെ വാദം തൃപ്തമാകുന്നു. പൊതുവെ പൂർവ്വമാതൃകകളെആശ്രയിച്ചായിരിക്കും ശാസ്ത്രത്തിലെ കണ്ടെത്തലുകൾ എന്നു പറഞ്ഞുകൊണ്ടാണുആര്യഭടന്റെയും ഭാസ്കരന്റെയും കൃതികളുടെ ഗ്രീക്ക് ഉത്ഭവത്തെക്കുറിച്ചുള്ളപഠനം വാൻ ഡെർ വേർഡെൻ അവസാനിപ്പിക്കുന്നത്.
ഒരു സ്ഥലത്തു നിന്ന് മറ്റൊരിടത്തേയ്ക്കുള്ള വിജ്ഞാനത്തിന്റെ സംപ്രക്ഷണത്തെക്കുറിച്ചുള്ള വാദങ്ങൾക്ക് രേഖാമൂലമുള്ളതെളിവുകൾ വേണമെന്ന് നിർബന്ധമില്ലായെന്നാണു ഈ ഉദാഹരണങ്ങളിൽ നിന്നും നാംകാണേണ്ടത്. പല കാരണങ്ങൾ കൊണ്ട് നശിച്ചുപോയവയായ പ്രാചീനകാലത്തെയുംമധ്യകാലത്തെയും നിരവധി ഗ്രന്ഥങ്ങളും രേഖകളും ഇന്ന് നിലവിലില്ല എന്നതാണുഇതിനു ആസ്പദമായിട്ടുള്ളത്. ഈ പരിതസ്ഥിതിയിൽ ആശയവിനിമയത്തിന്റെസഞ്ചാരമാർഗ്ഗങ്ങൾ, മുൻഗണനാക്രമങ്ങൾ, പദ്ധതിശാസ്ത്രസമാനതകൾ എന്നിവയാണുപടിഞ്ഞാറു നിന്നും കിഴക്കോട്ടുള്ള സംപ്രക്ഷണങ്ങളെക്കുറിച്ചുള്ള വാദങ്ങൾസ്ഥാപിക്കാൻ പരക്കെ അംഗീകരിക്കപ്പെട്ട തെളിവുകൾ. ഇവയെല്ലാം തന്നെലഭ്യമാണെങ്കിലും കേരളഗണിതത്തിന്റെ യൂറോപ്പിലേക്കുള്ള സഞ്ചാരത്തിനുപിന്നെയും ശക്തമായ തെളിവുകൾ ആവശ്യമുണ്ട്. ഗണിതശാസ്ത്രത്തിന്റെ ഇതുവരെയുള്ളചരിത്രപഠനങ്ങൾ മറിച്ചു നോക്കുന്ന ആർക്കും ഈയൊരു സഞ്ചാരത്തിന്റെസാധ്യതകളെക്കുറിച്ചുള്ള ആധികാരികമായി സൂചനകൾ അല്പം പോലും ലഭ്യമല്ല എന്നത്കാണാനാനും.
എങ്കിൽ കേരളീയഗണിതത്തിന്റെ സംപ്രക്ഷണത്തെക്കുറിച്ചുള്ള നമ്മുടെ അനുമാനങ്ങളെ എങ്ങനെയാണു സ്ഥാപിക്കാനാകുക? തങ്ങളുടെ പഠനങ്ങളുടെ മൂലശ്രോതസുകളെക്കുറിച്ച്മിക്കവാറും തന്നെ സൂചനകൾ നൽകുകയോ അവയ്ക്ക് കടപ്പാട് പരാമർശിക്കുകയോചെയ്യുന്ന രീതി മിക്കവാറും തന്നെ യൂറോപ്യൻ നവോത്ഥാനകാലത്തെഗണിതശാസ്ത്രജ്ഞന്മാർ അവലംബിച്ചിരുന്നില്ല. എന്നാൽ 1620കളുടെ തുടക്കം മുതൽ 1648 വരെ നടന്ന മാരിൻ മെഴ്സീൻ (Marin Mersenne) എന്ന സന്യാസിയുടെ ചിലപ്രവർത്തനങ്ങൾ കിഴക്കു നിന്നുള്ള ശാസ്ത്രീയ അറിവുകളുടെ സമാഹരണവുമായിബന്ധപ്പെട്ട സൂചനകൾ നൽകുന്നുണ്ട്.“ശാസ്ത്രത്തിന്റെ ആദ്യകാല റിപബ്ലിക്കിന്റെ സെക്രട്ടറി”എന്ന് വിശേഷിക്കപ്പെടാൻ അർഹതയുള്ളയാളായിരുന്നു മെഴ്സീൻ. പ്രമുഖനവോത്ഥാനകാല ഗണിതകാരന്മാരായ ദെക്കാർത്തെ, പാസ്കൽ, ഹോബ്സ്, ഫെർമാറ്റ്, രോബെർവാൽ എന്നിവരുമായി അദ്ദേഹം സമ്പർക്കം പുലർത്തിയിരുന്നു. ഒരു മിനിംസന്യാസിയായിരുന്നുവെങ്കിലും ജെസ്യൂട്ട് വിദ്യാഭ്യാസം സിദ്ധിച്ചിരുന്നമെഴ്സീൻ കൊളേജിയോ റൊമാനോയുമായും (Collegio Romano) ബന്ധം പുലർത്തിയിരുന്നു.ഗോവയുടെയും കൊച്ചിയുടെയും പ്രാധാന്യത്തെക്കുറിച്ച് അദ്ദേഹംബോധവാനായിരുന്നുവെന്ന് അദ്ദേഹത്തിന്റെ എഴുത്തുകുത്തുകൾസാക്ഷ്യപ്പെടുത്തുന്നുണ്ട് (ജ്യോതിശാസ്ത്രജ്ഞനായിരുന്ന ഇസ്മായിൽ ബോളിയഡ് (Ismael Boulliaud) റോമിലായിരുന്ന മെഴ്സീനു എഴുതിയ ഒരു കത്തിൽ).ബ്രാഹ്മണർക്കുണ്ടായിരുന്ന അറിവുകളെക്കുറിച്ചും“ഇൻഡിക്കോസി”നെക്കുറിച്ചുംഎഴുതിയ അദ്ദേഹം എർപെനെ (Erpen) പോലെയുള്ള പൗരസ്ത്യവാദക്കാരുടെ കൃതികളെവളരെ താല്പര്യത്തോടെയാണു സമീപിച്ചിരുന്നത് – എർപെന്റെ“les livres manuscrits Arabics, Syriaques, Persiens, Turcs, Indiens en langue Malaye”അന്നത് അദ്ദേഹം പരാമർശിക്കുന്നുണ്ട്.
1560 കൾക്കും 1650കൾക്കും ഇടയ്ക്ക് ഇന്ത്യൻ ഗണിതശാസ്ത്രത്തെക്കുറിച്ചുംജ്യോതിശാസ്ത്രത്തെക്കുറിച്ചും കലൻഡർ സമ്പ്രദായങ്ങളെക്കുറിച്ചുമുള്ള അറിവുകൾറോമിലെത്തുകയും അവിടെനിന്നും പാദുവ, പിസ എന്നിവ പോലുള്ള സമീപ ഇറ്റാലിയൻ സർവ്വകലാശാലകളിലേക്കുംപാദുവയിലേക്കെത്തിയിരുന്ന ജെയിംസ് ഗ്രിഗറിയെപ്പോലെയുള്ള സന്ദർശകർ വഴിയുംകവലെറി, ഗലീലിയോ എന്നിവർ വഴിയും ദൂരസ്ഥലങ്ങളിലേക്കുംപടർന്നിരിക്കാനും സാധ്യതയുണ്ട്. റോമിലെ ജെസ്യൂട്ടുകൾ വഴിയുംകേരളത്തെക്കുറിച്ച് മെഴ്സീൻ നേടിയിരുന്ന അറിവുകളായിരിക്കാം അദ്ദേഹത്തിന്റെവിഖ്യാതങ്ങളായ എഴുത്തുകുത്തുകൾ വഴി യൂറോപ്പിലാകെ പടർന്നത്. ഗലീലിയോപഠിപ്പിച്ചിരുന്ന പാദുവയിലെ തന്റെ നാലുവർഷത്തെ പ്രാവാസജീവിതകാലത്ത് ജെയിംസ്ഗ്രിഗറി സ്വായത്തമാക്കിയ ത്രികോണമിതിയെക്കുറിച്ചുള്ള അറിവുകൾ തീർച്ചയായുംഅത്തരമൊരു സാധ്യതയിലേക്ക് വിരൽ ചൂണ്ടുന്നുണ്ട്.
ഇവയെല്ലാം സന്ദർഭാനുസരണം പറഞ്ഞതാണു–കേരളീയ ഗണിതത്തിന്റെ സംപ്രക്ഷണത്തെക്കുറിച്ച് നമുക്ക് കൂടുതൽ ശക്തമായ മാനദണ്ഡങ്ങൾ ഉപയോഗിക്കാം.നോഗെബൗറിന്റെമാനദണ്ഡങ്ങളായ മുൻഗണനാക്രമം, ആശയവിനിമയപാതകൾ, പദ്ധതിശാസ്ത്ര സമാനതകൾഎന്നിവ കൂടാതെ സംപ്രക്ഷണത്തെക്കുറിച്ചുള്ള അനുമാനത്തെ ജെസ്യൂട്ട് മിഷണറിമാർവഴി നടന്ന ഈ പടർച്ചയെക്കുറിച്ചുള്ള തെളിവുകളുടെയും പ്രേരകങ്ങളുടെയുംഅടിസ്ഥാനത്തിൽ പരീക്ഷണവിധേയമാക്കുകയും കൂടി ചെയ്യാം എന്ന് ഞങ്ങൾ മുന്നോട്ട്വയ്ക്കുന്നു. മുന്നോട്ടുള്ള ഭാഗത്ത് ഇവ ചർച്ച ചെയ്യപ്പെടുന്നതാണു
4. കേരളീയ കലനത്തിന്റെ യൂറോപ്പിലേക്കുള്ള സംപ്രക്ഷണം: കാലാടിസ്ഥാനത്തിലുള്ളമുൻഗണനാക്രമം, ആശയവിനിമയപാതകൾ, പദ്ധതിശാസ്ത്രപരമായ സമാനതകൾ.
ന്യൂട്ടണുംലയ്ബ്നിസിനും മുൻപ് തന്നെ കലനശാസ്ത്രത്തിൽ കേരളീയമായവികാസങ്ങളുണ്ടായിരുന്നു എന്നത് ഇന്ന് നിസ്തർക്കമാണു. കേരളീയഗണിതത്തിലെആദ്യവും മൗലികവുമായ ആശയങ്ങൾക്ക് നാം കടപ്പെട്ടിരിക്കുന്നത് മാധവനോടാണു (1340-1425). ഈ ആശയങ്ങൾ നാം മുൻപ് പറഞ്ഞതുപോലെ pഎന്ന സംഖ്യയ്ക്കും ചില ത്രികോണമിതി ഫലനങ്ങൾക്കും ഒരു അനന്തശ്രേണി അവകലനവും ലഭ്യമാക്കുന്നതിനു കാരണമായി. ഈ വികാസപരിണാമങ്ങൾ അതിനാൽ തന്നെ ന്യൂട്ടൺന്റെയും ലയ്ബ്നിസിന്റെയും 17ആം നൂറ്റാണ്ടിലെ കലനത്തെക്കാൾ 250 വർഷമെങ്കിലും പഴയതായിരിക്കണം.
ദക്ഷിണേന്ത്യയുംഅറേബ്യൻ ഉൾക്കടലും (ബസ്ര തുറമുഖം വഴി) തമ്മിൽ ബന്ധിപ്പിക്കുന്ന ഒരു പാതനൂറ്റാണ്ടുകളായി നിലവിലുള്ളതാണു. 1499ൽ വാസ്കോ ദി ഗാമ മലബാർ കടപ്പുറത്ത്കാലു കുത്തിയത് ലിസ്ബൺ വഴി കേരളവുമായി നേരിട്ടൊരു പാത സൃഷ്ടമാകാൻകാരണമായി. അങ്ങനെ, 1499 ശേഷം, അതിന്റെ ഭൂമിശാസ്ത്രപരമായ കിടപ്പു മൂലംഇന്ത്യയുടെ ബാക്കി ഭാഗങ്ങളുമായി അത്ര എളുപ്പത്തിൽ ആശയവിനിമയം സാധ്യമല്ലാഞ്ഞകേരളം എന്നാൽ ലോകത്തിന്റെ ബാക്കി ഭാഗങ്ങളുമായി, പ്രത്യേകിച്ച്യൂറോപ്പുമായി നേരിട്ട് ഒരു ബന്ധം സ്ഥാപിച്ചു.
കാലക്രമമനുസരിച്ചുള്ളമുൻഗണന, ആശയവിനിമയ പാതകൾ എന്നിവ എളുപ്പത്തിൽ സ്ഥാപിക്കാമെങ്കിലുംപദ്ധതിശാസ്ത്രപ്രകാരമുള്ള സമാനതകൾ സ്ഥാപിക്കുന്നതിനായി കൂടുതൽ ചർച്ചകൾആവശ്യമാണു. ആദ്യമായി കാണേണ്ടത് കലനശാസ്ത്രത്തോട്യുക്തിഭാഷപ്രകടിപ്പിക്കുന്ന സമീപനത്തിനു സമാനമാണു ഫെർമാറ്റ്, പാസ്കൽ, വാല്ലിസ് മുതലായവർ കൈക്കൊണ്ടിരുന്ന സമീപനം എന്നതാണു.യുക്തിഭാഷയിൽ ഈ പറയുന്ന നിർണ്ണായക ഫലം തെളിയിച്ചിട്ടുമുണ്ട്.
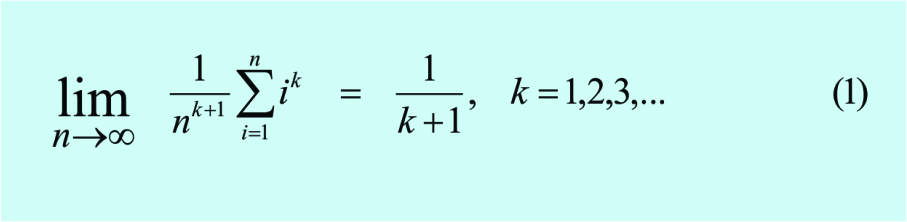
ഇതേ ഫലം തന്നെയാണു 17-ആം നൂറ്റാണ്ടിൽ ഫെർമാറ്റ്, പാസ്കൽ, വാല്ലിസ് മുതലായവർ y=xk എന്ന പരവലയങ്ങൾ (parabolas) ആദേശം ചെയ്യുന്ന വിസ്തീർണ്ണം നിർണ്ണയിക്കുന്നതിനും അല്ലെങ്കിൽ അതേ പോലെ തന്നെ∫ xk dx എന്നത് തിട്ടപ്പെടുത്താനു ഉപയോഗിച്ചിട്ടുള്ളത്. ഇവിടെശ്രദ്ധിക്കേണ്ടത് യുക്തിഭാഷയിലേതിനു സമാനമായ അനുമാനപദ്ധതിയാണു വാല്ലിസ് ഉപയോഗിക്കുന്നത് എന്നത് കേരളഗണിതത്തിന്റെ സംപ്രക്ഷണം എന്ന നമ്മുടെ വിഷയത്തെ സാധൂകരിക്കുന്നു എന്നതാണു. അതായത്n2എന്ന പദത്തിനു പകരം വാല്ലിസ്n(n + 1) ഉപയോഗിക്കുമ്പോൾ അദ്ദേഹം അർത്ഥമാക്കുന്നത്n അനന്തതയിലേക്ക് നീങ്ങുമ്പോൾ(n + 1) എന്ന പദത്തെn കൊണ്ട് പകരം വയ്ക്കാമെന്നതിനാൽn(n + 1) » n2 [1][1]എന്ന ഏകദേശം ഉപയോഗിക്കാൻ കഴിയും എന്നാണു. (replaces the term n2 by n(n + 1) implicitly implying that, as n tends to infinity, (n + 1) can be replaced by n so that he can use the approximation n(n + 1) » n2 ).കേരളീയഗണിതം അടിസ്ഥാനമാക്കിയിരിക്കുന്ന ഗണിതത്തിന്റെ ആര്യഭടമുറയും നവോത്ഥാനകാല ഗണിതകാരന്മാരുടെ രീതികളും തമ്മിലുള്ള പദ്ധതിശാസ്ത്രപ്രകാരമായ സമാനതകൾ വിരളമല്ല. രണ്ട് ഉദാഹരണങ്ങൾ കൂടി നോക്കാം.
സതതഭിന്നങ്ങളുടെ (continued fraction) സംവ്രജനങ്ങൾ (convergents) ചില ബന്ധങ്ങൾതൃപ്തിപ്പെടുത്തുന്നുണ്ട് എന്ന് 1655ൽ ജോൻ വാലിസ് തന്റെ‘അരിത്മെറ്റിക ഇൻഫിനിറ്റോറ’ത്തിൽ (Arithmetica Infinitorum )പ്രസ്താവിക്കുകയുണ്ടായി. കൃത്യം ഇതേ ആവർത്തനബന്ധങ്ങളെക്കുറിച്ച് ഒരു 500 വർഷമെങ്കിലും മുൻപ്ഭാസ്കരൻ രണ്ടാമൻ തന്റെ ബീജഗണിതം എന്ന കൃതിയിൽ കണ്ടെത്തിയിരുന്നു.കോണപരിച്ഛേദങ്ങളെക്കുറിച്ചുള്ള (angular sections) തന്റെ പ്രബന്ധത്തിൽപൈതഗോറസ് സിദ്ധാന്തത്തിന്റെ ഭാസ്കരൻചമച്ച രീതിയിലുള്ള തെളിവുകളാണു വാല്ലിസ് നിരത്തുന്നതെന്നതിൽ കവിഞ്ഞ ഒരുയാദൃശ്ചികതയാകാം ഇത് എന്ന് പറയാൻ നിർവാഹമില്ല. ബ്രെസിൻസ്കിയുടെ (Brezinski) അഭിപ്രായത്തിൽ വാല്ലിസ് സ്വതന്ത്രമായിട്ടായിരിക്കാം ആ ഫലങ്ങൾകണ്ടെത്തിയത്. എങ്കിലും ഭാസ്കരന്റെ പഠനങ്ങൾ അവിടേക്ക്എത്തിച്ചേർന്നിരിക്കാനുള്ള സാധ്യതയെക്കുറിച്ചും അദ്ദേഹം പ്രത്യേകംസൂചിപ്പിക്കുന്നു.
ഭാസ്കരന്റെ പഠനങ്ങളുമായുള്ള മറ്റൊരു സാമ്യം ഫെർമാറ്റ് 1657ൽ ഉയർത്തിയ ഒരു പ്രശ്നോത്തരിയാണു–“61 കൊണ്ട് ഗുണിച്ച് ഒന്ന് കൂട്ടിയാൽ ഒരു വർഗ്ഗസംഖ്യ കിട്ടുന്ന ഏറ്റവും ചെറിയ വർഗ്ഗസംഖ്യയ്ക്ക് ഏതാണു ഉദാഹരണം?”സ്ട്രൂയിക് (Struik) ചൂണ്ടിക്കാട്ടുന്നത് പോലെ ഇന്ത്യൻ ഗണിതകാരന്മാർ അതിനോടകം തന്നെ ആ പ്രശ്നത്തിനു പരിഹാരം കണ്ടെത്തിയിരുന്നു.A= 61 എന്നതിന്റെ പരിഹാരത്തിനുള്ള ഉദാഹരണം ഭാസ്കരൻ രണ്ടാമന്റെബീജഗണിതത്തിൽ കാണാം. അതിന്റെ ഫലനിർണ്ണയത്തിൽ വലിയ സംഖ്യകൾ [x = 1,766,319,049, y = 226,153,980] ഉൾപ്പെടുന്നു എന്നതിനാൽ ഈ യാദൃശ്ചികത നിസാരമായി കാണാൻ കഴിയുന്ന ഒന്നല്ല.ഇതേ പോലൊരു പ്രശ്നോത്തരി ഏഴാം നൂറ്റാണ്ടിൽ ബ്രഹ്മഗുപ്തൻഅവതരിപ്പിച്ചിട്ടുണ്ട്. ഭാസ്കരൻ രണ്ടാമൻ ഇതിനു സാമാന്യമായ പരിഹാരംകണ്ടെത്തുന്നത് അദ്ദേഹത്തിന്റെചക്രവാളരീതിയനുസരിച്ചാണു. അങ്ങനെ ഈ പ്രശ്നോത്തരി ഫെർമാറ്റും ഇന്ത്യൻ ഗണിതവും തമ്മിലുള്ള ബന്ധത്തെ സൂചിപ്പിക്കുന്നുണ്ട്.
5. കേരളഗണിതത്തിന്റെ യൂറോപ്പിലേക്കുള്ള സംപ്രക്ഷണം: സംപ്രക്ഷണത്തിനുസഹായകമായി ജെസ്യൂട്ട് മിഷണറിമാർ നടത്തിയ പ്രവർത്തനങ്ങൾക്ക് നിദാനമായപ്രേരകവും അത് സംബന്ധിച്ച തെളിവുകളും.
പ്രേരണ: കലണ്ടറിനുംജ്യോതിശാസ്ത്രത്തിനും കൂടുതൽ കൃത്യതയാർന്ന കണക്കുകൂട്ടലുകൾ (ഗണിതചരിത്രകാരൻ നല്ല ഉറപ്പോടെ ഇത് സാക്ഷ്യപ്പെടുത്തുന്നുണ്ട്) എന്നലക്ഷ്യമാണു ഇന്ത്യയിൽ നിന്ന് യൂറോപ്പിലേക്ക് വിജ്ഞാനം ഇറക്കുമതി ചെയ്യുന്നതിനു പ്രേരകമായത്.
ഉദാഹരണത്തിനു 16-ആം നൂറ്റാണ്ടിന്റെ പകുതിയോടെ നിലവിലിരുന്ന ജൂലിയൻ കലണ്ടർഉപയോഗിച്ചുകൊണ്ടുള്ള കണക്കുകൂട്ടലുകളിൽ ഒരു തെറ്റ് കടന്നുവന്നിരുന്നു.കണക്കാക്കിയിരുന്ന 365.25 ദിനങ്ങളെക്കാൾ 11.25 മിനിട്ടുകൾ കുറവായിരുന്നുവാസ്തവത്തിൽ ഒരു സൗരവർഷം. തത്ഫലമായി ഈ പിശക് കൂടി കൂടി ഈട്ടംകൂടുകയുംഈസ്റ്റർ ദിനം യഥാർത്ഥമായ ദിനത്തിൽ നിന്ന് ഗണ്യമായ രീതിയിൽ മാറുകയുംചെയ്തുവന്നു. ഉദാഹരണത്തിനു കലണ്ടർ പ്രകാരം മാർച്ച് 21-നുഉണ്ടാകേണ്ടിയിരുന്ന മഹാവിഷുവം അഥവാ മേഷാദി (vernal equinox) മാർച്ച് 11 –നായി മാറി. അങ്ങനെ, തെറ്റുതിരുത്തലില്ലായെങ്കിൽ വസന്തകാലത്ത് വന്ന്ചേരേണ്ട ഈസ്റ്റർ വേനൽകാലത്ത് വരുന്ന അവസ്ഥ വന്ന് ചേർന്നു. വിയെറ്റിന്റെ (Viete) ഗ്രീഗോറിയൻ കലണ്ടർ പരിഷ്കരണത്തിന്മേലുള്ള വിമർശത്തിൽഉപയോഗിച്ചിരിക്കുന്ന ഇന്ത്യൻ കലണ്ടർ പദമായ‘തിഥി’ഇതിനു നിദാനമാണു.
മറ്റൊന്ന്ജ്യോതിശാസ്ത്രത്തിൽ കേരളഗണിതകാരനായിരുന്ന നീലകണ്ഠൻ അവതരിപ്പിച്ചഗ്രഹമാതൃകയും പിന്നീട് ടയ്കോ ബ്രാഹെ അവതരിപ്പിച്ച മാതൃകയും തമ്മിലും 10-ആംനൂറ്റാണ്ടിലെ ഇന്ത്യൻ ജ്യോതിശാസ്ത്രകാരനായ്ഇരുന്ന മുൻജലന്റെ ചാന്ദ്രമാതൃകയെ അധികരിച്ചെന്നോണം കെപ്ലർ മുന്നോട്ട് വച്ച മാതൃകയും തമ്മിലുള്ളസാമ്യങ്ങളാണു.
ജെസ്യൂട്ട് മിഷണറിമാരുടെ സംപ്രക്ഷണപ്രവൃത്തികൾക്കുള്ള തെളിവുകൾ: ഫ്രാൻസിസ് ക്സേവിയറിന്റെ 1540-ലെ ഗോവയിലേക്കുള്ള വരവ് മലബാറിൽജെസ്യൂട്ടുകളുടെ 1670 വരെയുള്ള തുടർച്ചയായുള്ള സാന്നിധ്യത്തിനു കാരണമായി.ആദ്യകാല ജെസ്യൂട്ടുകൾ തദ്ദേശീയഭാഷകൾ പഠിക്കുന്നതിലും വിവർത്തനങ്ങളിലുംമാത്രം താല്പര്യപ്പെട്ടിരുന്നപ്പോൾ 1578 ശേഷം വന്ന മിഷണറിമാർവ്യത്യസ്തരായിരുന്നു. കൊളേജിയോ റൊമാനോയിൽ ക്ലാവിയസ് അവതരിപ്പിച്ച പുതിയഗണിതശാസ്ത്രസമ്പ്രദായത്തിലെ ആദ്യ ബാച്ചിൽ പരിശീലനം സിദ്ധിച്ചയാളായിരുന്നപ്രസിദ്ധനായ മറ്റിയോ റിച്ചി (Matteo Ricci) വിദഗ്ദ്ധനായ ഒരു ഗണിതശാസ്ത്രജ്ഞനായിരുന്നു. 1578ൽഇന്ത്യയിലെത്തുന്നതിനു മുൻപ് ലിസ്ബണിൽ നിന്നും റിച്ചി പ്രപഞ്ചശാസ്ത്രവുംപ്രകൃതിശാസ്ത്രവും അഭ്യസിച്ചിരുന്നു. തദ്ദേശീയമായ അറിവുകൾനേടിയെടുക്കുന്നതിലുള്ള ജെസ്യൂട്ടുകളുടെ ലക്ഷ്യത്തെ സംബന്ധിച്ചിടത്തോളംറിച്ചിയുടെ ഗോവയിലേക്കുള്ള വരവ് പ്രധാനമായിരുന്നു. ഗണിതം, പ്രപഞ്ചശാസ്ത്രം, ജ്യോതിശാസ്ത്രം, കപ്പൽ യാത്ര എന്നിവയിലുള്ള പ്രത്യേകമായ ജ്ഞാനം കോളണികളുടെഅറിവുകൾ കണ്ടെത്താനുള്ള ആളായി റിച്ചിയെ ചുമതലപ്പെടുത്താൻ പോന്നതായിരുന്നു.ഇന്ത്യൻ ശാസ്ത്രത്തെക്കുറിച്ച് അന്വേഷണങ്ങൾ നടത്താൻ അദ്ദേഹത്തിനു പ്രത്യേകനിർദ്ദേശങ്ങളുണ്ടായിരുന്നു.
തുടർന്ന്, ക്ലാവിയസോ ഗ്രീൻബെർഗറോ ( ക്ലാവിയസിനു ശേഷം കൊളേജിയോ റോമാനോയിലെ പ്രഫെസർ)പരിശീലിപ്പിച്ച നിരവധി ജെസ്യൂട്ട് ശാസ്ത്രജ്ഞന്മാർ ഇന്ത്യയിലേക്ക്അയക്കപ്പെട്ടു. അവരുടെ ശാസ്ത്രവൃത്തികളുടെ അടിസ്ഥാനത്തിൽ, അവരിൽ ഏറ്റവുംശ്രദ്ധിക്കപ്പെടേണ്ടവർ ജൊഹാൻ ഷ്രെക്കും (Johann Schreck)അന്റോണിയോ റുബീനോയുമാണു (Antonio Rubino). ബീജഗണിതത്തിലും ജ്യാമിതിയിലുമുള്ള പഠനങ്ങളുടെ പേരിൽ പ്രശസ്തനായവിയെറ്റിന്റെ സഹപാഠിയായിരുന്നു ജൊഹാൻ ഷ്രെക്ക്. ഇന്ത്യയിലെ അവരുടെതാമസക്കാലത്ത് കൊച്ചിയുൾപ്പടെയുള്ള മലബാർ പ്രദേശങ്ങളിലേക്കും അവർ യാത്രചെയ്തു. കൊച്ചിയായിരുന്നു അന്ന് അനന്താംശ കലനശാസ്ത്രത്തിലെ വികാസപരിണാമങ്ങളുടെ (infinitesimal calculus)പ്രഭവകേന്ദ്രം. ഈ പറഞ്ഞ എല്ലാ ജെസ്യൂട്ട് പണ്ഡിതരും പ്രാദേശികവിജ്ഞാനംസ്വാംശീകരിക്കാൻ വളരെ യത്നിച്ചിരുന്നു എന്നത് നമുക്ക് പിന്നീട്ദർശിക്കാവുന്നതാണു. ഈസ്റ്ററും മറ്റ് ഉത്സവദിനങ്ങളും തെറ്റ് കൂടാതെകണക്ക്ആക്കാനുള്ള പള്ളിയുടെ ആഗ്രഹപ്രകാരമാണു ആ ജെസ്യൂട്ടുകൾ കലണ്ടർസംബന്ധിച്ച് പ്രത്യേക താല്പര്യമെടുത്തത് എന്ന് നമുക്ക് തൽക്കാലംചൂണ്ടിക്കാട്ടാം. ക്ലാവിയസായിരുന്നു 1582-ലെ ഗ്രിഗോറിയൻ കലണ്ടർ പരിഷ്കരണ കമ്മീഷൺ തലവൻ. ഈ ജെസ്യൂട്ടുകൾ ഇന്ത്യ, ചൈന എന്നീ പ്രദേശങ്ങളും യൂറോപ്പും തമ്മിലുള്ള ശാസ്ത്രവിഷയങ്ങളിലെ കൊടുക്കൽവാങ്ങലുകളുടെ ഭാഗമായിരുന്നു എന്നാണു ചിലരുടെ അഭിപ്രായം.
പ്രാദേശികഅറിവുകൾ സ്വായത്തമാക്കുക എന്ന പ്രത്യേക ലക്ഷ്യവുമായി 15-ആം നൂറ്റാണ്ടിന്റെഅവസാനത്തോടെയും 16-ആം നൂറ്റാണ്ടിന്റെ ആരംഭത്തിലുമായി ഇന്ത്യയിലേക്ക്എത്തിച്ചേർന്ന ഗണിതശാത്രവിശാരദന്മാരായ ഒരു സംഘം ജെസ്യൂട്ടുകൾ ഉണ്ടെന്ന് നാംപരാമർശിക്കുകയുണ്ടായി. നമ്മൾ പ്രത്യേകം ശ്രദ്ധിക്കേണ്ടത് കേരളീയഗണിതശാഖപ്രധാനമായും ജ്യോതിഷസംബന്ധമായ പ്രവചനങ്ങൾക്കായുള്ള ജ്യോതിശാസ്ത്രപഠനവുമായിബന്ധപ്പെട്ടായിരുന്നു എന്നതാണു. അതുമൂലം തന്നെ ജ്യോതിശാസ്ത്രവും കലണ്ടർവിജ്ഞാനവുമായി ബന്ധപ്പെട്ടുകൊണ്ട് കലനശാസ്ത്രത്തിലെ വിദ്യകൾ യൂറോപ്പിലേക്ക്പടർത്താൻ ജെസ്യൂട്ടുകൾക്ക് പ്രേരണയും അവസരവുമുണ്ടായി എന്നാണു നമ്മുടെഅനുമാനം.
മലബാർ തീരത്തെ ആദ്യകാല ജെസ്യൂട്ടുകളുമായി ബന്ധപ്പെട്ട് വിക്കിയുടെ (Wicki)ചരിത്രസംബന്ധിയായ പഠനങ്ങളിലെ പല സൂചനകളിൽ നിന്നും നമുക്ക് കാണാൻ കഴിയുന്നത് പ്രകാരംഅവരെല്ലാം തന്നെ ഗണിതത്തിലും ജ്യോതിശാസ്ത്രത്തിലും ആ ദേശത്തിന്റെസമയസൂക്ഷിപ്പിലും താല്പര്യമുള്ളവരായിരുന്നുവെന്നാണു. പ്രാദേശിക ഭാഷകളായതമിഴും മലയാളവും പഠിക്കുക വഴി അവർ ഈ അറിവുകൾ നല്ല രീതിയിൽസ്വായത്തമാക്കുകയും ചെയ്തു. അവരുടെ ശാസ്ത്രവും സംസ്കാരവും ആചാരവുംപഠിച്ചുകൊണ്ട് തദ്ദേശീയരെ ജെസ്യൂട്ട് കത്തോലിക്കാമതത്തിലേക്ക് പരിവർത്തനംചെയ്യിക്കുക എന്ന ലക്ഷ്യത്തിലൂന്നിയാണു പ്രാദേശികഭാഷകളുടെ പഠനം നടന്നത്.ഉദാഹരണത്തിനു 1615-ൽ ഡീ നോബിലി (de Nobili) എന്ന ഒരു പ്രമുഖ ആദ്യകാല ജെസ്യൂട്ട് വരാഹമിഹിരന്റെവേദാംഗ ജ്യോതിഷത്തിനുഒരു വിമർശമെഴുതുകയുണ്ടായി. പ്രാദേശിക വിജ്ഞാനങ്ങളായ ജ്യോതിഷവും മറ്റുംമ്ലബാർ തീരത്തെ ജെസ്യൂട്ട് കോളേജുകളുടെ സിലബസിൽ ഉൾപ്പെടുത്തുക വഴി ഈ രീതിഒരു വിദ്യാഭ്യാസനയമാക്കാനും അവർ ശ്രമിച്ചിരുന്നു എന്നാണു കരുതാനാകുക..ആദ്യകാല ജെസ്യൂട്ടുകൾ ഈ പ്രാദേശിക അറിവുകൾ യൂറോപ്പിലേക്ക് പടർത്തുന്നതിലും ക്രിയാത്മകമായ പങ്ക് വഹിച്ചിരുന്നു. ഇതിനു തെളിവുകൾ റോമിലെ ജെസ്യൂട്ട് ചരിത്ര ലൈബ്രറിയിലുള്ള (ARSI) ഗോവ38, 46, 58എന്നീ ശേഖരങ്ങളിൽ ലഭ്യമാണു. അവസാനത്തെ ശേഖരത്തിൽ മലബാറിലെ നിയമവ്യവസ്ഥ, ശാസ്ത്രങ്ങൾ, യന്ത്രകലകൾ എന്നിവയെക്കുറിച്ച് ഫ. ഡിയോഗോ ഗോൺസാൽവസ്രേഖപ്പെടുത്തിയിരിക്കുന്നത് കാണാം. യൂറോപ്പിലേക്കുള്ള സംപ്രക്ഷണത്തിനുമുൻപ് തന്നെ പ്രാദേശിക അറിവുകൾ യൂറോപ്യൻ ഭാഷകളിലേക്ക് തർജ്ജമചെയ്യപ്പെട്ടിരുന്നതിന്റെ ഏറ്റവും മികച്ച ഉദാഹരണമാണു 1563ൽ ഗോവയിൽപ്രസിദ്ധീകരിക്കപ്പെട്ട ഗാർഷ്യാ ദ ഓർടയുടെ (Garcia da Orta) പ്രസിദ്ധമായColloquios dos simples e drogas he cousas mediçinas da India എന്നകൃതി. ഭാഷാപരവും ദേശീയവുമായ കാരണങ്ങളാൽ വിസ്മൃതിയിലാണ്ടു കിടക്കുന്ന ഇത്പോലുള്ള നിരവധി കൃതികൾ തീർച്ചയായും ഉണ്ടായിരിക്കേണ്ടതാണു.
ആദ്യകാലത്തെയുംഅവസാനകാലഘട്ടങ്ങളിലെയും ജെസ്യൂട്ടുകൾ പ്രാദേശിക ശാസ്ത്രപഠനങ്ങളിൽവ്യാപൃതരായിരുന്നുവെന്നുണ്ടെങ്കിൽ, അതിനു മധ്യേയുള്ള കാലഘട്ടങ്ങളിലെപ്രസിദ്ധരായ റിച്ചി, ഷ്രെക്ക്, റുബീനോ എന്നിവരുടെ അക്കാദമിക വൈദഗ്ദ്ധ്യംകണക്കിലെടുത്താൽ അനുമാനിക്കാവുന്നത് ഈ സംപ്രക്ഷണം ശക്തമായിനടന്നുകൊണ്ടിരുന്നിരിക്കണം എന്നാണു. തീർച്ചയായും ഇത് നടന്നിരുന്നു എന്നതിനുതെളിവുകളുണ്ട്. ഇന്ത്യൻ കലണ്ടർ ശാസ്ത്രത്തെക്കുറിച്ചുള്ളഅന്വേഷണങ്ങൾക്കിടയിൽ പ്രാദേശികമായ രീതിയിൽ സമയം അഥവാ ജ്യോതിഷം കണക്കുകൂട്ടുന്നതിനും രേഖപ്പെടുത്തുന്നതിനും തന്നെ സഹായിക്കുന്നതിനായി“ബുദ്ധിമാനായ ഒരു ബ്രാഹ്മണനെയോ സത്യസന്ധനായ ഒരു നാട്ടുകാരനെയോ”ആവശ്യമുണ്ട് എന്നാണു മാഫെയ്ക്കുള്ള (Maffei) ഒരു കത്തിൽ റിച്ചി പറയുന്നത്.മറ്റൊരിക്കൽ, 1580ൽ കൊല്ലത്ത് നിന്നും ഡി മെൻസെസ് (de Menses) രേഖപ്പെടുത്തുന്നത് പ്രാദേശിക അറിവുകളുടെ അടിസ്ഥാനത്തിൽ നോക്കിയാൽ യൂറോപ്യൻമാപ്പിംഗ് രീതികളിൽ തെറ്റുകളുണ്ടെന്നാണു. പിന്നീട് വന്ന നിരവധിജെസ്യൂട്ടുകളും ഇതേ രീതിയിൽ കലണ്ടർ വിജ്ഞാനത്തെക്കുറിച്ചും യൂറോപ്യൻ മാപ്പിംഗ് രീതികളിലും കണക്കുകൂട്ടൽ പട്ടികകളിലും പ്രാദേശികമായ അറിവുകളുടെ അടിസ്ഥാനത്തിൽ ശാസ്ത്രീയമായി അവർ കണ്ടെത്തിയ തെറ്റുകളെ കുറിച്ച് രേഖപ്പെടുത്തുന്നുണ്ട്. സമയം രേഖപ്പെടുത്താൻ ഉപയോഗിച്ചിരുന്ന യൂറോപ്യൻ പട്ടികകളിലെ തെറ്റുകുറ്റങ്ങളെക്കുറിച്ച് 1610-ൽ അന്റോണിയോ റുബീനോ എഴുതിയിരുന്നു. 1618-ലെഷ്രെക്കിന്റെ ഒരു കത്തിൽ കെപ്ലെറിന്റെ സിദ്ധാന്തങ്ങൾക്ക്ശക്തിയേകുന്നതിനായി ഇന്ത്യയിൽ നിന്നുള്ള നിരീക്ഷണങ്ങൾ ശേഖരിച്ച്സഹായിക്കുവാൻ പ്രമുഖ ജെസ്യൂട്ട് ഗണിതകാരനായ പോൾ ഗുൽഡിനോട്ആവശ്യപ്പെടുന്നുണ്ട്.
കേരളീയ ഗണിതം ഉൾപ്പെടുന്ന കയ്യെഴുത്തുരേഖകൾ ജെസ്യൂട്ടുകൾക്ക് ലഭ്യമായിരുന്നു എന്നതിനു ഇവയൊന്നും സാധൂകരണമായിരുന്നില്ല എന്ന് വന്നാലും പ്രാദേശികജ്യോതിഷത്തെയും കലണ്ടർ ശാസ്ത്രത്തെയും കുറിച്ചുള്ള അവരുടെ ശാസ്ത്രീയമായഅന്വേഷണങ്ങൾ ഈ ദിശയിലുള്ളറിവുകൾ അവർക്ക് നൽകിയിരുന്നു എന്നതിൽതർക്കമുണ്ടാകില്ല. ചിലസൂചനകൾ പ്രകാരം ബ്രാഹ്മണർ സ്വന്തം അറിവുകളിൽ ഒരുതരം രഹസ്യാത്മകത കാത്ത്സൂക്ഷിക്കുകയും അവ പകർന്ന് കൊടുക്കുന്നതിൽ വിമുഖത കാട്ടുകയും ചെയ്തിരുന്നു.എന്നാൽ നിരവധി ആളുകൾ ഈ അഭിപ്രായം പങ്കു വയ്ക്കാതെയും ഇരിക്കുന്നുണ്ട്.ഉദാഹരണത്തിനു മലയാളഭാഷ കൂടി പഠിച്ച പതിനേഴാം നൂറ്റാണ്ടിന്റെമധ്യകാലത്തുണ്ടായിരുന്ന ഫ. ഡിയോഗോ ഗോൺസാൽവസിനു മലബാറിലെനിയമവ്യവസ്ഥയെക്കുറിച്ചും ശാസ്ത്രങ്ങളെക്കുറിച്ചുംയന്ത്രകലകളെക്കുറിച്ചെഴുതാനും സാധിച്ചിരുന്നു. ഈ പുസ്തകം റന്മിലെ ജെസ്യൂട്ട് ചരിത്ര ലൈബ്രറിയിൽMS Goa 58 എന്ന ശേഖരത്തിൽ കാണാവുന്നതാണു. ശ്രദ്ധിക്കേണ്ട കാര്യം ഈ കാലയളവിൽ ഫ. ഫ്രോയിസിനു വേണ്ടി സംസ്കൃത കൃതികൾ വിവർത്തനം ചെയ്യുന്നതിനായി ഒരു ബ്രാഹ്മണൻ എട്ട് വർഷത്തോളം ചെലവിട്ടിരുന്നു എന്നതാണു.
അറിവ്സമ്പാദനത്തിനും സംപ്രക്ഷണത്തിനുമായി ജെസ്യൂട്ട് മിഷണറിമാർ നടത്തിയപ്രവർത്തനങ്ങൾ ഇതിനലൊക്കെത്തന്നെ നിസ്തർക്കമാണു. ഇതുകൂടാതെ 1580-ൽ പോർചുഗൽസ്പെയിനിന്റെ അധീനതയിലായതോടെ ഈ സംപ്രക്ഷണത്തിനു ലാഭം എന്ന മറ്റൊരു മാനംകൂടി കൈ വന്നു. ബൗദ്ധികമോ സാമ്പത്തികമോ–ലാഭം ഏത് വിധമായിരുനുവെന്നാലും പ്രസക്തമായ കേരളീയ ഗണിതശാസ്ത്രകൃതികൾ സമ്പാദിക്കുന്നതിനു പണ്ഡിതരായ ജെസ്യൂട്ടുകൾക്ക് ആ പ്രേരണ മാത്രം മതിയായിരുന്നിരിക്കണം.
6. ജെസ്യൂട്ടുകൾ കേരളീയ കലനശാസ്ത്രകൃതികൾ കൈവശമാക്കിയതിനുള്ള രീതിയെക്കുറിച്ച് ഒരു അനുമാനം:
കേരളീയ കലനശാത്രത്തിന്റെ സംപ്രക്ഷണത്തിൽ ജെസ്യൂട്ടുകൾക്കുള്ള പങ്ക് അംഗീകരിക്കാമെങ്കിലും എങ്ങനെയണവർ തന്ത്രസംഗ്രഹം, യുക്തിഭാഷമുതലായ പ്രധാന ഇന്ത്യൻ കൃതികൾ നേടിയെടുത്തത് എന്ന ചോദ്യം പ്രസക്തമായിതുടരും. പണ്ഡിതരായ ബ്രാഹ്മണരുമായോ ക്ഷത്രിയരുമായോ അടുത്ത ബന്ധംപുലർത്തിയിരുന്നുവെങ്കിൽ മാത്രമേ ജെസ്യൂട്ടുകൾക്ക് അത്സാധ്യമാകുമായിരുന്നുള്ളൂ. ഒരു പണ്ഡിതബ്രാഹ്മണൻ ജെസ്യൂട്ടുകൾക്കായി ജോലിചെയ്തിരുന്ന കാര്യം നാം മുകളിൽ കണ്ടിരുന്നു. ഇത് കൂടാതെ ജെസ്യൂട്ടുകൾകൊച്ചിയിലെ ക്ഷത്രിയ രാജാക്കന്മാരുമായി അടുത്ത രീതിയിൽ ആശയവിനിമയംനടത്തിയിരുന്നതെങ്ങനെ എന്ന് നമുക്ക് കാണാം. പണ്ഡിതരായ ആ രാജാക്കന്മാരുമായിപുലർത്തിയ ബന്ധമാണു ജെസ്യൂട്ടുകളെ കേരളീയ ഗണിതവുമായി അത്രയടുത്ത് ഇടപഴകൻ സഹായിച്ചത്.
മധ്യകാല കേരളീയ ഗണിതശാസ്ത്രത്തിലും ജ്യോതിശാസ്ത്രകൃതികളിലും വിശാരദരായിരുന്ന‘തമ്പുരാൻ’എന്ന ക്ഷത്രിയ വർമ്മ കുടുംബത്തിലെ അംഗങ്ങളായിരുന്നു കൊച്ചിയിലെരാജാക്കന്മാർ. സദ്-രത്നമാല എന്ന കൃതി രചിച്ച ശങ്കര വർമ്മതലശ്ശേരിക്കടുത്തുള്ള കടത്തനാട്ടിലെ രാജാവിന്റെ അനുജനായിരുന്നുവെന്നുംഅദ്ദേഹം ഒരു മികച്ച ഗണിതശാത്രജ്ഞനായിരുന്നുവെന്നും‘കേരളത്തിലെ സംസ്കൃതസാഹിത്യത്തിന്റെ ചരിത്രം’എന്ന കൃതിയിൽ ശ്രീനിവാസ അയ്യങ്കാർ രേഖപ്പെടുത്തിയിരിക്കുന്നത് ഇതിനു സാക്ഷ്യമാണു. കൊച്ചിരാജാവായിരുന്ന രാജവർമ‘കരണപദ്ധതിയിലെ’കാലഘടനിർണയത്തെക്കുറിച്ച് ജ്ഞാനമുണ്ടായിരുന്ന ആളായിരുന്നുവെന്നും അയ്യങ്കാർ എഴുതുന്നു. 1948-ൽ (എ. ആർ അഖിലേശ്വര അയ്യർക്കൊപ്പം)യുക്തിഭാഷയ്ക്ക് മലയാളത്തിൽ ഒരു വ്യാഖ്യാനമെഴുതിയത് കൊച്ചിയിലെ യുവരാജാവായിരുന്നരാമ വർമ തമ്പുരാനായിരുന്നു. കേരളീയ ഗണിതത്തെക്കുറിച്ച് പ്രസക്തങ്ങളായതാളിയോലകൾ തങ്ങൾക്ക് നൽകിയത് രാമ വർമ തമ്പുരാനായിരുന്നുവെന്ന്ൻ രാജഗോപാൽ, രംഗാചാരി എന്നിവർ പ്രസ്താവിക്കുന്നുണ്ട്. രാമവർമ മരു തമ്പുരാൻ കേരളീയജ്യോതിശാസ്ത്രത്തിനു നൽകിയ മികച്ച സംഭാവനകളെ കെ വെങ്കിടേശ്വര ശർമപ്രകീർത്തിക്കുന്നുണ്ട്. ജ്യോതിഷപ്രകാരമുള്ള പ്രവചനങ്ങൾക്ക് ആവശ്യം വേണ്ടജ്യോതിശാസ്ത്രത്തെയും ഇവ അടങ്ങിയ താലിയോലകളെക്കുറിച്ചും അത്യാവശ്യം വേണ്ടഅറിവെങ്കിലും കൊച്ചിരാജാക്കന്മാർക്കുണ്ടായിരുന്നുവെന്നു ആര്യഭടഫോറത്തിനെഴുതിയ ഒരു കത്തിൽ മുകുന്ദമാരാർ ( അവസാനത്തെ കൊച്ചിരാജാവിന്റെമൂത്ത പുത്രൻ) എഴുതിയിരിക്കുന്നു. അവരിൽ പലരും വിവിധ ഗണിതശാസ്ത്ര, ജ്യോതിശാസ്ത്ര കൃതികൾക്ക് ഭാഷ്യം എഴുതാൻ തക്ക പാണ്ഡിത്യമുള്ളവരായിരുന്നു.മുകുന്ദമാരാർ തന്നെ രാജഗോപാലും ഒന്നിച്ച് ഒരു പ്രബന്ധംപ്രസിദ്ധീകരിച്ചിട്ടുണ്ട്. ഇത് മാത്രമല്ല 19-ആംനൂറ്റാണ്ടിലെ ചാൾസ് വിഷ് മുതൽ 20-ആം നൂറ്റാണ്ടിലെ രാജഗോപാലും രംഗാചാരിയുംവരെ തങ്ങളുടെ കൈവശമുണ്ടായിരുന്ന കൃതികൾ തന്ന് സഹായിച്ചതിനുകൊച്ചിരാജകുടുംബത്തിലെ അംഗങ്ങളെ നന്ദിപൂർവ്വം സ്മരിക്കുന്നുണ്ട്.
അനവധിയായകൃതികളും താളിയോലകളും കൈവശമുണ്ടായിരുന്ന കൊച്ചിയിലെ പഴയ രാജകുടുംബംപാണ്ഡിത്യമുള്ളവർ മാത്രമായിരുന്നില്ലായെന്നും മറ്റു പണ്ഡിതരെ സഹായിക്കാൻഎന്നും തയ്യാറായിരുന്നുവെന്നുമാണു ഇവ കാണിക്കുന്നത്. അതിനാൽ രാജകുടുംബംതന്നെയായിരുന്നിരിക്കണം ജെസ്യൂട്ടുകൾക്ക് ലഭിച്ച അറിവുകളുടെ ശ്രോതസ്സ്.തീർച്ചയായും മലബാർ തീരത്ത് പ്രവർത്തിച്ചിരുന്ന ജെസ്യൂട്ടുകൾ കൊച്ചിരാജാവുമായി അടുത്തബന്ധം പുലർത്തിയിരുന്നു. മാത്രമല്ല, പൊതിവിൽ പരിവർത്തനത്തിനുഎതിരായിരുന്നുവെങ്കിലു തന്റെ കുടുംബത്തിലെ ആളുകൾക്ക് ക്രിസ്ത്യൻ മതംസ്വീകരിക്കാൻ അനുവാദം കൊടുത്ത രാമ വർമ രാജാവ് 1670-കളിൽ ജെസ്യൂട്ടുകൾക്ക്പ്രത്യേക അവകാശങ്ങളും നൽകുകയുണ്ടായി. രാമവർമ തന്റെ നികുതിപിരുവുകാരനായി ഒരുപോർചുഗീസുകാരനെ നിയമിക്കുക വഴി കൊച്ചി രാജാവും പോർചുഗീസുകാരുമായിഉണ്ടായിരുന്ന അടുത്ത ബന്ധം ഒന്നുകൂടി ഉറച്ചിരുന്നു. അവർ തമ്മിൽനിലവിലിരുന്ന ഈ അടുത്ത ബന്ധവും, ജെസ്യൂട്ടുകൾക്ക് ഇന്ത്യൻജ്യോതിശാസ്ത്രത്തിലുണ്ടായിരുന്ന താല്പര്യവും, കൊച്ചി രാജകുടുംബത്തിനുഅവയിലുണ്ടായിരുന്ന പാണ്ഡിത്യവും ചേർത്ത് വെച്ച് നോക്കുമ്പോൾജെസ്യൂട്ടുകൾക്ക് പ്രധാനപ്പെട്ട കൃതികൾ ലഭിച്ചത് രാജകുടുംബത്തിൽ നിന്ന്തന്നെയാകും എന്നാണു അനുമാനിക്കാൻ കഴിയുക.
7. ഉപസംഹാരം:കേരളത്തിൽ നിന്ന് നേരിട്ട് യൂറോപ്പിലേക്ക് നടന്ന സംപ്രക്ഷണത്തിനുള്ള തെളിവുകളിലാണു നാമിവിടെ ശ്രദ്ധ കേന്ദ്രീകരിച്ചത്. എന്നാൽബാലസുബ്രഹ്മണ്യം ചൂണ്ടിക്കാട്ടിയിട്ടുള്ളത് പോലെ കരകൗശലക്കാരുംസാങ്കേതികവിദഗ്ദ്ധരും അടങ്ങിയ ഒരു സംഘം പണിത സാങ്കേതികജഞാനവും കണക്കുകൂട്ടൽവിദ്യകളിലും ഉൾപ്പെടുന്ന ഒരു വഴിയിലും കൂടിയായിരിക്കാം കേരളീയഗണിതത്തിന്റെ കണ്ടെത്തലുകൾ പടർന്നത്. ജെസ്യൂട്ട് ആശയവിനിമയങ്ങൾതെളിയിക്കുന്ന രേഖകളുടെ അപര്യാപ്തതയെ ഇത് ന്യായീകരിക്കുന്നു.സമുദ്രായനത്തിനും മാപ്പ് നിർമ്മാണത്തിനും കലണ്ടർ നിർമ്മാണത്തിനുംസഹായിക്കുന്ന യൂറോപ്യൻ ഗ്രന്ഥങ്ങളിൽ അവയ്ക്ക് സഹായകമായത് കേരളീയഗണിതത്തിന്റെ കണ്ടെത്തലുകളാണു എന്നതിനു സൂചനകൾ ഉണ്ടായിരുന്നുവെങ്കിൽ കൂടി ആകാര്യം യൂറോപ്യൻ ഗണിതകാരന്മാരുമായി നേരിട്ട് പങ്കുവയ്ക്കപ്പെട്ടുകാണുകയില്ല. കരകൗശല- സാങ്കേതിക വിദഗ്ദ്ധരായ നിർമാതാക്കൾസൈദ്ധാന്തികപ്രശ്നങ്ങളിലുപരി പ്രായോഗികതയിൽ ശ്രദ്ധകേന്ദ്രീകരിക്കുന്നവരായതിനാൽ യൂറോപ്പിലെ പ്രശസ്തരായ ഗണിതകാരന്മാരെവായിച്ചിട്ടുണ്ടാകാൻ സാധ്യതയില്ല. ഇനി അഥവാ വായിച്ചിരുന്നുവെങ്കിൽ കൂടി ആവായനകൾ അത്ര ഗൗരവതരമായിരുന്നിരിക്കുകയുമില്ല. ഈ വിധമുള്ള വളരെതാല്പര്യമുണർത്തുന്ന ഒരു അനുമാനത്തെക്കുറിച്ച് കൂടുതൽ വിവരങ്ങൾബാലസുബ്രഹ്മണ്യത്തിന്റെ കൃതിയിൽ വായിക്കാവുന്നതാണു.
2002-2005 കാലഘട്ടത്തിൽ കേരളീയ ഗണിതത്തെക്കുറിച്ചു നടത്തിയ ഒരു അന്വേഷണപരിപാടിക്ക് സഹായം നൽകിയAHRB-യെ (Arts and Humanities Research Board) ലേഖകർ നന്ദിപൂർവ്വം സ്മരിക്കുന്നു. AHRB പ്രൊജക്റ്റിനു മുൻപായി സി കെ രാജു നൽകിയ വിവരങ്ങൾക്കും നന്ദിപ്രകടിപ്പിക്കുന്നു. ഈപഠനത്തിന്റെ ഭാഗങ്ങൾ 2001 സെപ്റ്റംബറിൽ മെക്സിക്കോ സിറ്റിയിൽ നടന്ന XXI-ആമത് അന്താരാഷ്ട്ര ശാസ്ത്രചരിത്ര കോൺഫറൻസിലും ലേഖകർ പ്രസിദ്ധീകരിച്ച“ഗണിതശാസ്ത്രചരിത്രത്തിലെ യൂറോകേന്ദ്രീകരണം–കേരളീയശാഖയെ പറ്റി ചിലത്, വംശവും വർഗ്ഗവും, 2004, 45(4), 45-59.”എന്നിവയിൽ ഉൾപ്പെടുത്തിയിട്ടുണ്ട്.
———————————————
ഡെന്നിസ് ഫ്രാൻസിസ് അൽമെയ്ഡ
എക്സെറ്റെർ സർവകലാശാല, യു കെ
[email protected]
&
ജോർജ് ഗീവർഗീസ് ജോസഫ്
മാഞ്ചസ്റ്റർ സർവകലാശാല
[email protected]
(വിവർത്തനം: സ്വാതി ജോർജ്)







Be the first to write a comment.